目录
你是否曾经为开发复杂的工业自动化界面而头疼?传统的WinForms控件在面对实时动画、物理模拟和复杂图形渲染时显得力不从心。想要实现流畅的传送带动画、精确的机械臂控制,还要保证系统的响应性和稳定性,这些挑战让许多C#开发者望而却步。
本文将通过一个完整的工业自动化模拟系统案例,手把手教你使用SkiaSharp + WinForms构建高性能的2D动画引擎。你将学会如何优雅地处理实时渲染、状态管理、物理模拟等核心技术问题,最终掌握工业级界面开发的核心技能,当然这就是一个简单的仿真。
🎯 核心技术架构分析
📊 系统架构设计
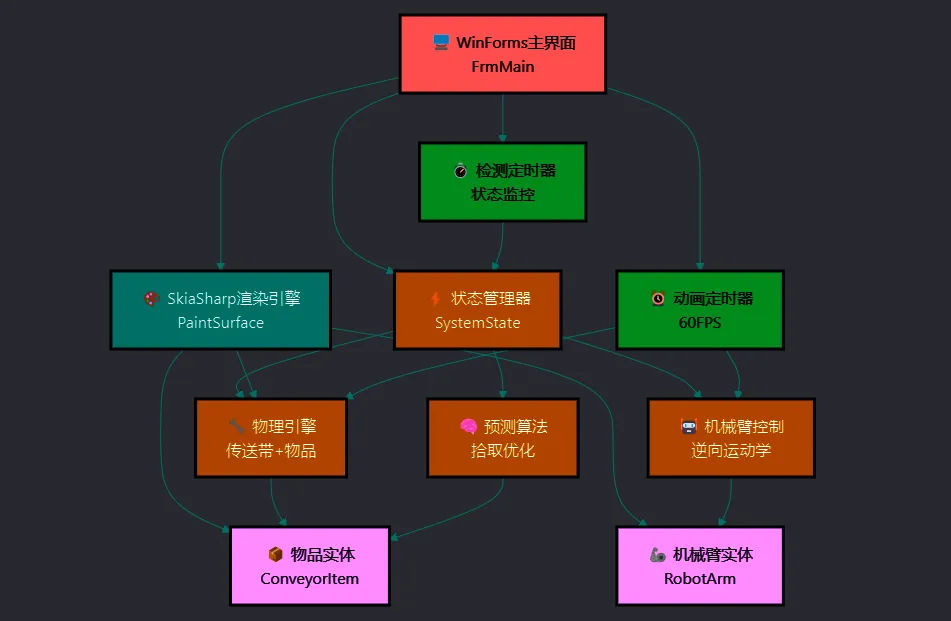
现代工业界面开发面临三大核心挑战:性能瓶颈、状态复杂性和渲染效率。传统的控件绘制方式无法满足实时动画的需求,我们需要一套全新的解决方案。
c#// 🔥 核心渲染引擎设计
public partial class FrmMain : Form
{
// 分离关注点:状态管理
private SystemState currentState = SystemState.Idle;
private LightStatus currentLight = LightStatus.Gray;
// 物理引擎:传送带系统
private float conveyorSpeed = 20.0f;
private float conveyorAcceleration = 10.0f;
private float currentSpeed = 0.0f;
// 实体管理:对象池模式
private List<ConveyorItem> items = new List<ConveyorItem>();
// 智能控制:预测算法
private readonly float PICKUP_TIME_ESTIMATE = 2.0f;
private readonly float DETECTION_TO_PICKUP_DISTANCE = 120.0f;
}
基本类
c#using SkiaSharp;
namespace AppSimulation
{
public class ConveyorItem
{
private static int _idCounter = 1;
public string Id { get; private set; }
public SKPoint Position { get; set; }
public SKSize Size { get; set; }
public float Speed { get; set; }
public bool IsBeingPicked { get; set; }
public bool IsTargeted { get; set; }
public DateTime CreatedTime { get; private set; }
public ConveyorItem()
{
Id = $"Item_{_idCounter:D3}";
_idCounter++;
CreatedTime = DateTime.Now;
IsBeingPicked = false;
IsTargeted = false;
}
public SKRect GetBounds()
{
return new SKRect(
Position.X - Size.Width / 2,
Position.Y - Size.Height / 2,
Position.X + Size.Width / 2,
Position.Y + Size.Height / 2
);
}
public bool IntersectsWith(SKRect rect)
{
return GetBounds().IntersectsWith(rect);
}
}
}
c#using SkiaSharp;
namespace AppSimulation
{
public class RobotArm
{
public SKPoint BasePosition { get; set; }
public float Link1Length { get; set; }
public float Link2Length { get; set; }
public float Joint1Angle { get; set; }
public float Joint2Angle { get; set; }
// 关节角度限制(弧度)
public float Joint1MinAngle { get; set; } = -MathF.PI;
public float Joint1MaxAngle { get; set; } = MathF.PI;
public float Joint2MinAngle { get; set; } = -MathF.PI / 2;
public float Joint2MaxAngle { get; set; } = MathF.PI / 2;
public SKPoint GetJoint1Position()
{
return new SKPoint(
BasePosition.X + Link1Length * MathF.Cos(Joint1Angle),
BasePosition.Y + Link1Length * MathF.Sin(Joint1Angle)
);
}
public SKPoint GetEndEffectorPosition()
{
var joint1Pos = GetJoint1Position();
return new SKPoint(
joint1Pos.X + Link2Length * MathF.Cos(Joint1Angle + Joint2Angle),
joint1Pos.Y + Link2Length * MathF.Sin(Joint1Angle + Joint2Angle)
);
}
public bool IsAngleValid(float j1, float j2)
{
return j1 >= Joint1MinAngle && j1 <= Joint1MaxAngle &&
j2 >= Joint2MinAngle && j2 <= Joint2MaxAngle;
}
public float GetReach()
{
return Link1Length + Link2Length;
}
public bool IsPositionReachable(SKPoint target)
{
var dx = target.X - BasePosition.X;
var dy = target.Y - BasePosition.Y;
var distance = MathF.Sqrt(dx * dx + dy * dy);
var maxReach = Link1Length + Link2Length;
var minReach = MathF.Abs(Link1Length - Link2Length);
return distance >= minReach && distance <= maxReach;
}
}
}
🛠️ 五大核心解决方案
🎮 方案一:高性能渲染引擎
问题:传统GDI+在复杂动画场景下性能不足,帧率低下影响用户体验。
解决方案:基于SkiaSharp的硬件加速渲染管道
c#private void SkiaViewMain_PaintSurface(object sender, SKPaintSurfaceEventArgs e)
{
var canvas = e.Surface.Canvas;
canvas.Clear(new SKColor(30, 30, 30));
// 🚀 关键优化:分层渲染,减少重绘开销
DrawConveyor(canvas); // 背景层
DrawDetectionZone(canvas); // 交互层
DrawItems(canvas); // 动态层
DrawRobotArm(canvas); // 前景层
DrawInformationText(canvas); // UI层
}
// 💡 性能优化技巧:画笔复用
private void InitializePaints()
{
paintConveyor = new SKPaint
{
Color = SKColors.DarkSlateGray,
Style = SKPaintStyle.Fill,
IsAntialias = true // 开启抗锯齿
};
// ⚠️ 注意:记得在Form关闭时释放资源
// paintConveyor?.Dispose();
}
实战要点:
- 使用
IsAntialias = true提升视觉效果 - 合理复用画笔对象,避免频繁创建销毁
- 分层渲染策略,只重绘必要区域
⚡ 方案二:智能状态机管理
问题:复杂系统状态切换混乱,容易出现状态不一致问题。
解决方案:基于枚举的状态机模式
c#public enum SystemState
{
Idle, // 灰色 - 待机
Detecting, // 黄色 - 检测到物品
Picking, // 绿色 - 拾取中
Processing // 蓝色 - 处理中
}
// 🎯 状态驱动的业务逻辑
private void TimerDetection_Tick(object sender, EventArgs e)
{
bool itemDetected = CheckItemInDetectionZone();
switch (currentState)
{
case SystemState.Idle:
if (itemDetected)
{
currentState = SystemState.Detecting;
currentLight = LightStatus.Yellow;
lblStatusLight.Text = "检测到物品";
UpdateStatusLight(); // 立即更新UI
}
break;
case SystemState.Detecting:
if (!itemDetected && !isPickingInProgress)
{
currentState = SystemState.Idle;
currentLight = LightStatus.Gray;
lblStatusLight.Text = "待机状态";
UpdateStatusLight();
}
break;
}
}
最佳实践:
- 每个状态都有明确的进入和退出条件
- 使用
switch语句确保所有状态都被处理 - UI更新与状态变更同步进行
🔧 方案三:精确的逆向运动学算法
问题:机械臂控制需要从末端位置反推关节角度,数学计算复杂。
解决方案:几何学+三角函数的逆向运动学解算
c#private (float J1, float J2, bool success) CalculateInverseKinematics(SKPoint target)
{
var dx = target.X - robotArm.BasePosition.X;
var dy = target.Y - robotArm.BasePosition.Y;
var distance = MathF.Sqrt(dx * dx + dy * dy);
// 🎯 关键算法:约束处理
float maxReach = robotArm.Link1Length + robotArm.Link2Length;
float minReach = MathF.Abs(robotArm.Link1Length - robotArm.Link2Length);
if (distance > maxReach) distance = maxReach - 5;
else if (distance < minReach) distance = minReach + 5;
// 📐 余弦定理求解关节2角度
var cosJ2 = (distance * distance - robotArm.Link1Length * robotArm.Link1Length - robotArm.Link2Length * robotArm.Link2Length) / (2 * robotArm.Link1Length * robotArm.Link2Length);
cosJ2 = MathF.Max(-1.0f, MathF.Min(1.0f, cosJ2)); // 防止数值误差
var j2 = -MathF.Acos(cosJ2); // 选择肘部向下配置
// 🎯 关节1角度计算
var beta = MathF.Atan2(robotArm.Link2Length * MathF.Sin(j2), robotArm.Link1Length + robotArm.Link2Length * MathF.Cos(j2));
var alpha = MathF.Atan2(dy, dx);
var j1 = alpha - beta;
bool valid = robotArm.IsAngleValid(j1, j2);
return (j1, j2, valid);
}
技术亮点:
- 数值稳定性处理:使用
MathF.Max/Min防止acos参数越界 - 多解选择:优先选择肘部向下的自然配置
- 安全检查:验证计算结果是否在有效范围内
🎬 方案四:流畅的动画插值系统
问题:机械运动需要平滑过渡,避免突兀的瞬间变化。
解决方案:基于时间的平滑插值算法
c#private async Task<bool> AnimateRobotToPosition(SKPoint targetPos, int durationMs)
{
var startTime = DateTime.Now;
var startAngles = new { J1 = robotArm.Joint1Angle, J2 = robotArm.Joint2Angle };
var (targetJ1, targetJ2, success) = CalculateInverseKinematics(targetPos);
try
{
while ((DateTime.Now - startTime).TotalMilliseconds < durationMs)
{
float progress = (float)(DateTime.Now - startTime).TotalMilliseconds / durationMs;
progress = Math.Min(1.0f, progress);
// 🌟 关键:平滑插值函数
float smoothProgress = SmoothStep(progress);
var newJ1 = Lerp(startAngles.J1, targetJ1, smoothProgress);
var newJ2 = Lerp(startAngles.J2, targetJ2, smoothProgress);
robotArm.Joint1Angle = newJ1;
robotArm.Joint2Angle = newJ2;
RequestCanvasRefresh();
await Task.Delay(16); // 约60FPS
}
return true;
}
catch (Exception)
{
return false;
}
}
// 🎨 平滑插值函数:实现缓入缓出效果
private float SmoothStep(float t) => t * t * (3.0f - 2.0f * t);
private float Lerp(float start, float end, float t) => start + (end - start) * t;
动画优化策略:
SmoothStep函数提供自然的缓动效果- 固定16ms间隔确保60FPS流畅度
- 异步执行避免阻塞UI线程
🧠 方案五:智能预测拾取算法
问题:动态环境下需要预测物体未来位置,实现精确拾取。
解决方案:基于运动学的预测算法
c#private SKPoint? CalculatePredictedPickupPosition(ConveyorItem item)
{
if (item.Speed <= 0) return null;
// 🎯 预测核心:考虑机械臂动作时间
float pickupTime = PICKUP_TIME_ESTIMATE;
float travelDistance = item.Speed * pickupTime;
var predictedX = item.Position.X + travelDistance;
// ⚠️ 边界检查:确保预测位置在工作范围内
if (predictedX > 100 && predictedX < 700)
{
return new SKPoint(predictedX, item.Position.Y);
}
return null;
}
// 🚀 三种拾取策略的智能选择
private bool ShouldStartPicking(ConveyorItem item)
{
return currentPickingMode switch
{
PickingMode.Static => IsInOptimalStaticPosition(item), // 停带拾取
PickingMode.Dynamic => IsInOptimalDynamicPosition(item), // 跟随拾取
PickingMode.Predictive => IsInOptimalPredictivePosition(item), // 预测拾取
_ => false
};
}
算法优势:
- 多策略支持:静态、动态、预测三种模式
- 实时适应:根据物体速度和位置智能选择
- 容错机制:边界检查确保系统稳定性
运行界面
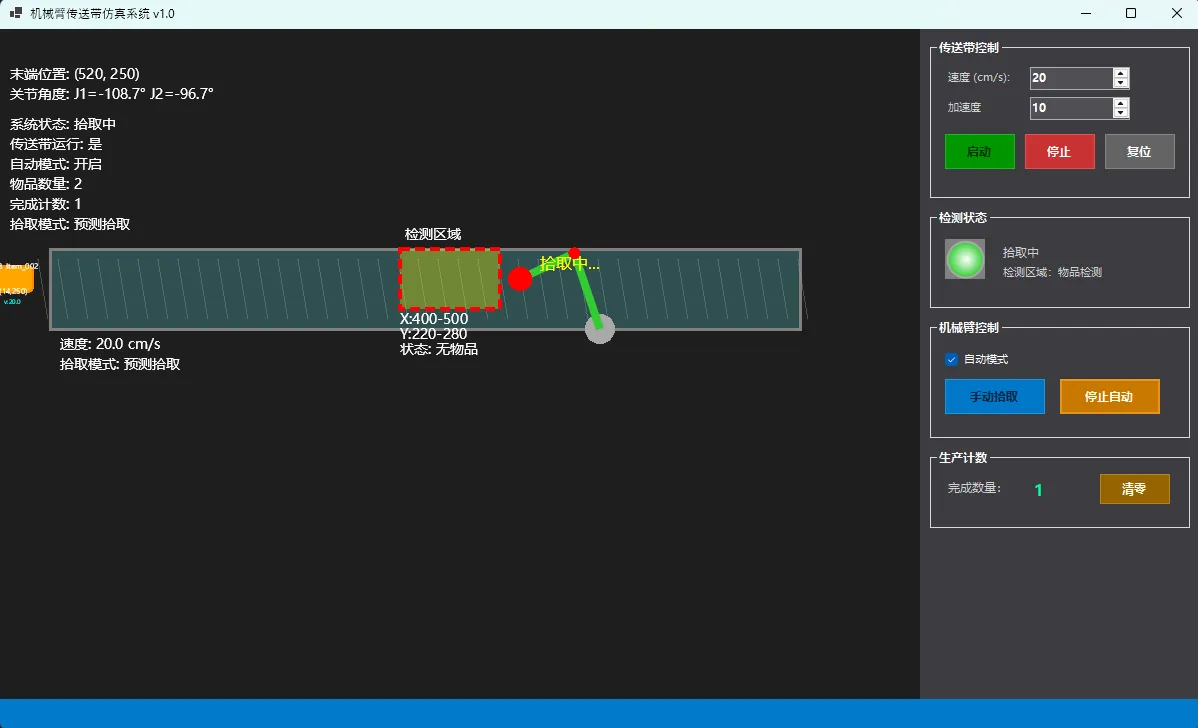
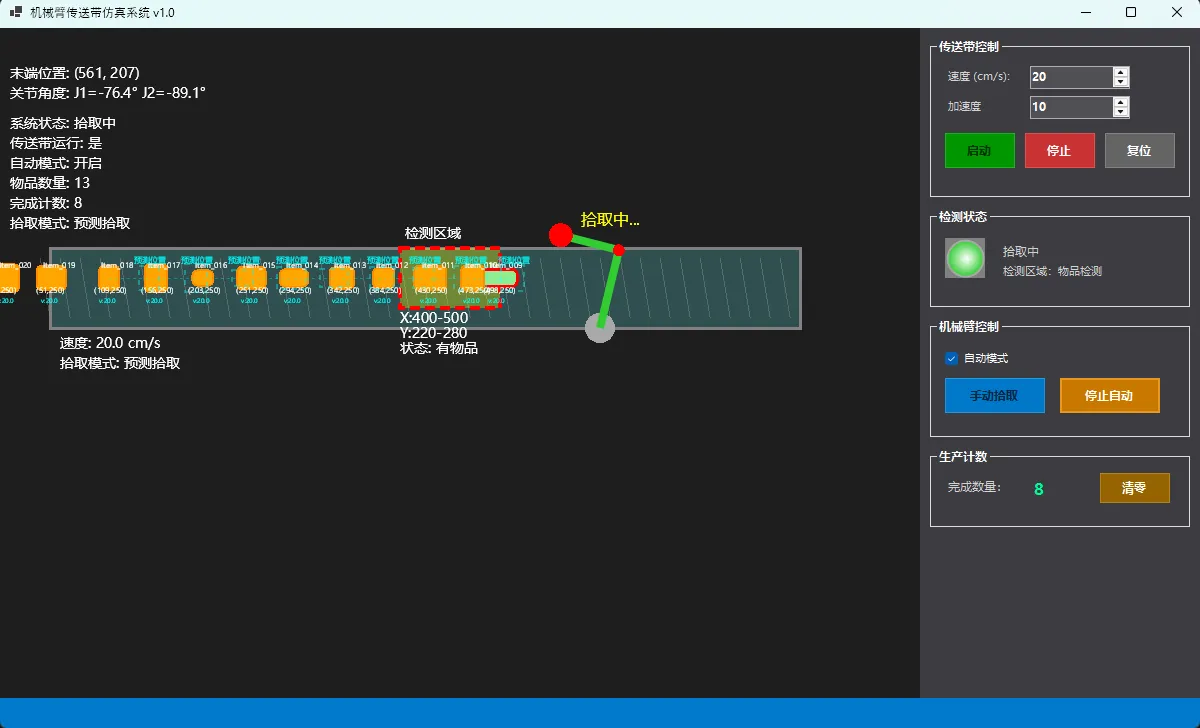
📈 性能优化核心技巧
🔥 关键优化点
- 画笔资源管理:预创建并复用SKPaint对象
- 分层渲染:只重绘变化的图层
- 时间控制:使用高精度时间戳避免帧率不稳定
c#// 💡 性能监控:精确的时间控制
private DateTime lastAnimationTimestamp = DateTime.Now;
private void TimerAnimation_Tick(object sender, EventArgs e)
{
var now = DateTime.Now;
// 🎯 关键:动态时间步长,确保动画稳定性
float deltaTime = Math.Clamp((float)(now - lastAnimationTimestamp).TotalSeconds, 0.016f, 0.1f);
lastAnimationTimestamp = now;
UpdateItems(deltaTime);
UpdateRobotArmAnimation(deltaTime);
skiaViewMain.Invalidate();
}
🎊 总结与展望
通过本文的深入分析,我们掌握了工业级2D动画系统的三个核心要点:
- 架构设计:分层渲染 + 状态机管理,确保系统的可维护性和扩展性
- 算法实现:逆向运动学 + 预测算法,实现精确的机械控制
- 性能优化:资源复用 + 时间控制,保证60FPS流畅体验
这套解决方案不仅适用于工业自动化界面,还可以扩展到游戏开发、数据可视化、科学计算等多个领域。SkiaSharp的跨平台特性让你的应用可以轻松移植到不同操作系统。
掌握了这些技术,你就拥有了开发复杂交互式界面的核心能力。是否想要将这些技术应用到你的项目中?在评论区分享你的具体需求,让我们一起探讨更多的实现细节!
觉得这篇文章对你有帮助吗?请转发给更多需要的同行,让我们一起推动C#技术社区的发展!
关注我们,获取更多C#实战技巧和项目源码! [ref:1,2,4]
本文作者:技术老小子
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!