二叉树是一种常见的数据结构，它在编程中有着广泛的应用，如搜索算法、排序算法、决策树等。在C#中实现二叉树涉及到对节点的定义、树的构建和树的遍历。本文将详细介绍如何在C#中实现一个二叉树。

二叉树节点的定义

首先，我们需要定义一个二叉树节点。每个节点包含一个数据元素以及两个指向子节点的引用。

C#
public class BinaryTreeNode<T>
{
    public T Value { get; set; }
    public BinaryTreeNode<T> Left { get; set; }
    public BinaryTreeNode<T> Right { get; set; }

    public BinaryTreeNode(T value)
    {
        Value = value;
        Left = null;
        Right = null;
    }
}

在这个类中，T是一个泛型类型，这意味着我们的二叉树可以存储任何类型的数据。Value属性用于存储节点的数据，Left和Right属性分别用于引用节点的左子节点和右子节点。

构建二叉树

构建二叉树通常从创建根节点开始，然后递归地创建左子树和右子树。

C#
public class BinaryTree<T>
{
    public BinaryTreeNode<T> Root { get; set; }

    public BinaryTree(T rootValue)
    {
        Root = new BinaryTreeNode<T>(rootValue);
    }

    // 添加节点、删除节点等方法可以在这里实现
}

在BinaryTree类中，我们定义了一个Root属性，它代表树的根节点。构造函数允许我们创建一个二叉树并初始化其根节点。

遍历二叉树

遍历二叉树是指按照某种顺序访问树中的每个节点。下面是三种基本的遍历方式：

前序遍历 (Pre-order)

先访问当前节点，然后递归地进行前序遍历左子树，最后递归地进行前序遍历右子树。

C#
public void PreOrderTraversal(BinaryTreeNode<T> node)
{
    if (node != null)
    {
        Console.WriteLine(node.Value); // 访问节点
        PreOrderTraversal(node.Left);  // 遍历左子树
        PreOrderTraversal(node.Right); // 遍历右子树
    }
}

中序遍历 (In-order)

先递归地进行中序遍历左子树，然后访问当前节点，最后递归地进行中序遍历右子树。

C#
public void InOrderTraversal(BinaryTreeNode<T> node)
{
    if (node != null)
    {
        InOrderTraversal(node.Left);   // 遍历左子树
        Console.WriteLine(node.Value); // 访问节点
        InOrderTraversal(node.Right);  // 遍历右子树
    }
}

后序遍历 (Post-order)

先递归地进行后序遍历左子树，然后递归地进行后序遍历右子树，最后访问当前节点。

C#
public void PostOrderTraversal(BinaryTreeNode<T> node)
{
    if (node != null)
    {
        PostOrderTraversal(node.Left);  // 遍历左子树
        PostOrderTraversal(node.Right); // 遍历右子树
        Console.WriteLine(node.Value);  // 访问节点
    }
}

实例：构建和遍历二叉树

现在我们创建一个二叉树实例，并进行遍历。

C#
class Program
{
    static void Main(string[] args)
    {
        // 创建二叉树
        BinaryTree<int> tree = new BinaryTree<int>(1);
        tree.Root.Left = new BinaryTreeNode<int>(2);
        tree.Root.Right = new BinaryTreeNode<int>(3);
        tree.Root.Left.Left = new BinaryTreeNode<int>(4);
        tree.Root.Left.Right = new BinaryTreeNode<int>(5);

        // 执行遍历
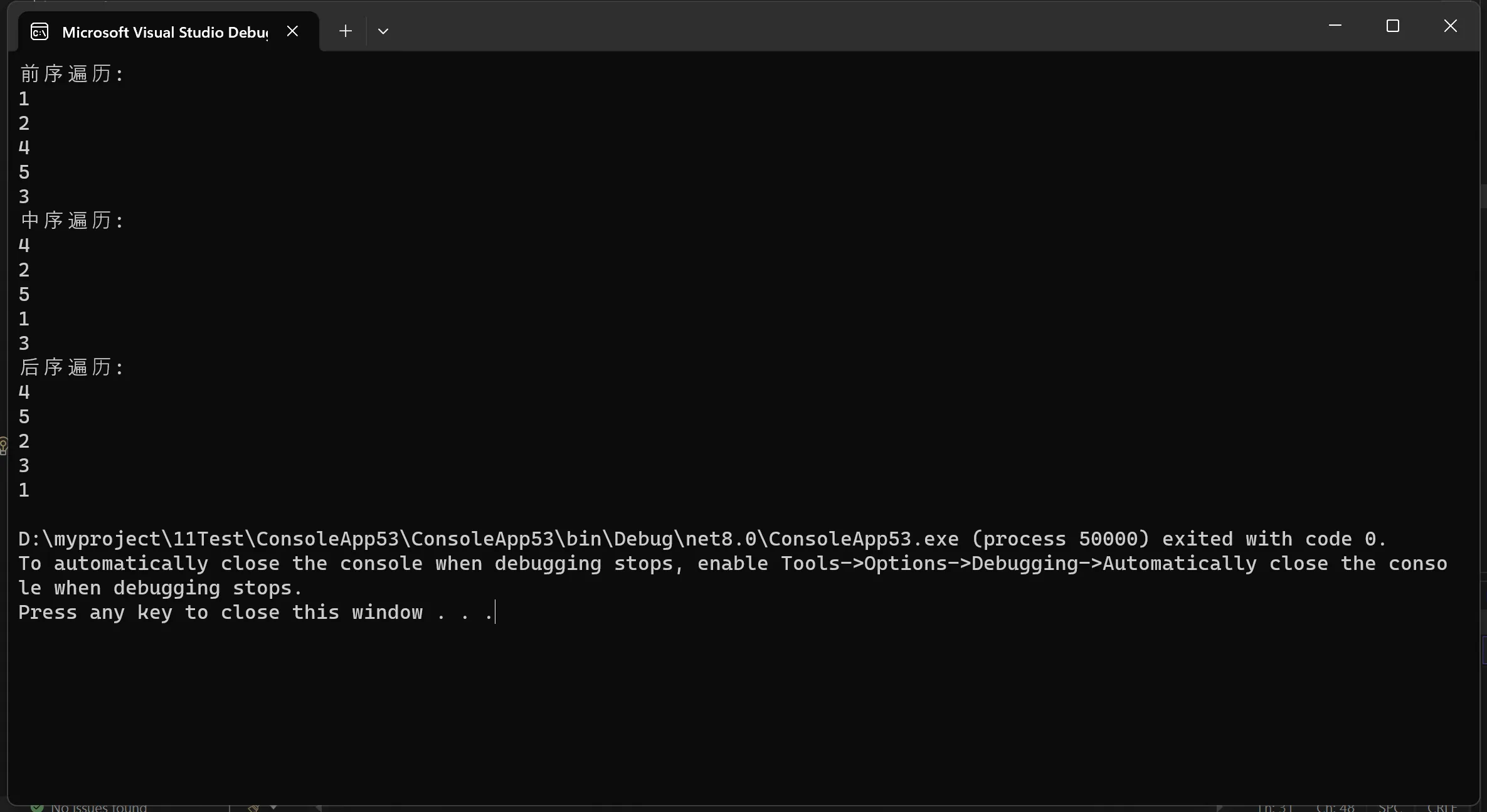
        Console.WriteLine("前序遍历:");
        tree.PreOrderTraversal(tree.Root);

        Console.WriteLine("中序遍历:");
        tree.InOrderTraversal(tree.Root);

        Console.WriteLine("后序遍历:");
        tree.PostOrderTraversal(tree.Root);
    }
}

结论

在C#中实现二叉树结构涉及到创建节点类、构建树以及通过不同方式遍历树。理解这些基本概念和操作是学习更高级的树结构和算法的基础。通过实践这些概念，开发者可以更好地利用二叉树来解决实际问题。

目录