在工业物联网时代,你是否还在为老旧串口设备无法直接接入网络而头疼?是否因为复杂的协议转换而加班到深夜?今天,我将用一个完整的C#项目,手把手教你构建一个高性能的串口转以太网转换器,让传统设备秒变智能终端!
这不仅仅是一个简单的转换工具,更是一套完整的工业级解决方案,包含多客户端管理、异步数据处理、实时状态监控等企业级功能。无论你是嵌入式工程师还是.NET开发者,这篇文章都将为你打开工业互联的新世界!
🎯 问题分析:工业现场的真实痛点
传统串口设备的困境
在工厂自动化中,大量PLC、传感器、仪表等设备仍使用RS232/RS485串口通信。这些设备面临的核心问题:
- 距离限制:串口通信距离通常不超过15米
- 单点连接:一个串口只能连接一个设备
- 维护困难:布线复杂,故障排查耗时
- 扩展性差:无法直接接入现代网络系统
现有解决方案的不足
市面上的串口服务器虽然能解决基本需求,但存在明显短板:
- 成本高昂:工业级产品动辄几千元
- 功能单一:缺乏灵活的数据处理能力
- 集成困难:难以与现有系统无缝对接
💡 解决方案:C#打造的智能转换器
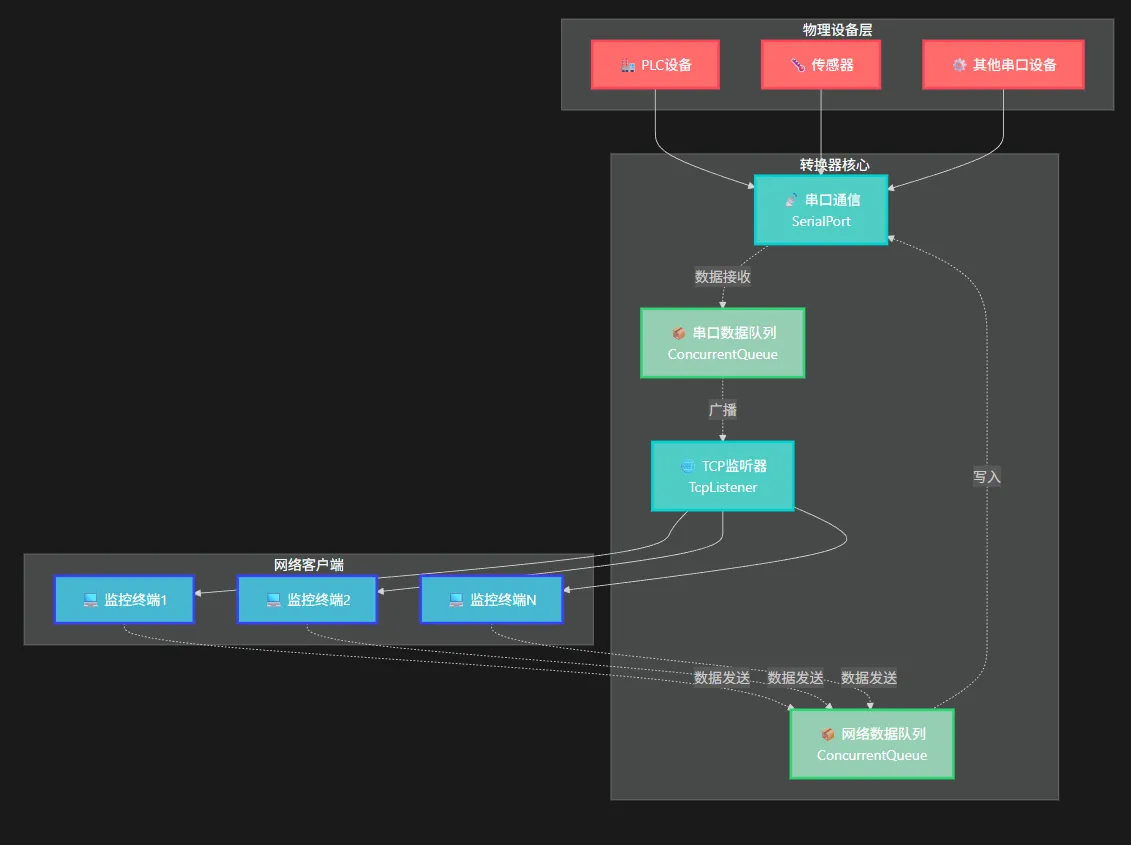
核心架构设计
我们的解决方案采用生产者-消费者模式,通过并发队列实现高效的双向数据转换:
还在用繁琐的Process类执行命令行操作吗?还在为进程输出重定向、错误处理、异步执行而头疼吗?今天为大家介绍一个游戏规则改变者:CliWrap,一个专为C#开发者打造的命令行交互库,让你的代码更简洁、更安全、更强大!
🔍 痛点分析:为什么需要CliWrap?
传统Process类的问题
使用原生Process类执行命令行操作时,开发者经常遇到以下痛点:
- 代码冗长复杂:需要大量样板代码处理进程启动、输出重定向
- 死锁风险:不当的流处理容易导致进程hang住
- 异步支持差:缺乏现代化的异步/等待支持
- 错误处理繁琐:退出码判断、异常处理逻辑分散
- 管道操作困难:多进程链式调用实现复杂
CliWrap的优势
- ✅ 流式API设计:链式配置,代码直观易读
- ✅ 完全异步:原生支持async/await模式
- ✅ 智能管道系统:轻松实现进程间数据传输
- ✅ 多执行模式:缓冲、事件流、管道等灵活选择
- ✅ 安全性保障:自动参数转义,防止注入攻击
📦 安装与配置
Bash# NuGet包管理器
Install-Package CliWrap
# .NET CLI
dotnet add package CliWrap
兼容性:
- .NET Standard 2.0+
- .NET Core 3.0+
- .NET Framework 4.6.2+
- 跨平台支持(Windows、Linux、macOS)
💡 解决方案:5个实用技巧让你快速上手
🎯 技巧1:基础命令执行
传统Process方式(代码冗长):
C#var process = new Process
{
StartInfo = new ProcessStartInfo
{
FileName = "git",
Arguments = "status",
UseShellExecute = false,
RedirectStandardOutput = true
}
};
process.Start();
var output = process.StandardOutput.ReadToEnd();
process.WaitForExit();
CliWrap方式(简洁优雅):
C#using System.Diagnostics;
using CliWrap;
namespace AppCliWrap
{
internal class Program
{
static async Task Main(string[] args)
{
var result = await Cli.Wrap("git")
.WithArguments(["status"])
.WithWorkingDirectory("D:\\myproject\\18csharp-code")
.ExecuteAsync();
// 自动包含进程信息
Console.WriteLine($"退出码: {result.ExitCode}");
Console.WriteLine($"执行时间: {result.RunTime}");
}
}
}
你是否还在为繁琐的库存管理而头疼?每天面对枯燥的CRUD操作,重复输入商品信息,手动查询库存状态?
今天,我将带你用C#和Semantic Kernel打造一个革命性的智能库存管理系统。想象一下,只需要说"帮我添加一个iPad Pro,价格8999元,库存20台",系统就能自动完成所有操作!
这不是科幻,而是我们今天要实现的真实项目。通过WPF界面+AI对话,让传统的管理系统焕发新生命力。无论你是C#新手还是资深开发者,这套解决方案都将为你的项目带来质的飞跃!
🎯 痛点分析:传统库存管理的三大难题
1. 操作繁琐,效率低下
传统系统需要逐个字段填写,步骤冗长,容易出错。一个简单的添加商品操作可能需要点击7-8次才能完成。
2. 查询复杂,信息孤立
想要了解库存状况,需要在多个界面间切换,数据缺乏关联性分析,决策效率低。
3. 学习成本高,用户体验差
新员工需要培训才能熟练操作系统,界面复杂,功能分散。
💡 革命性解决方案:AI对话式管理
🔥 核心优势
- 自然语言交互:告别复杂表单,用说话的方式管理数据
- 智能分析建议:AI自动分析库存状况,提供专业建议
- 一句话操作:复杂的业务逻辑通过简单对话完成
🛠️ 技术架构解析
核心技术栈
- 前端:WPF + MVVM模式
- AI引擎:Microsoft Semantic Kernel
- 大模型:DeepSeek API(兼容OpenAI格式)
- 数据绑定:ObservableCollection实时更新
🏗️ 系统架构图

"程序又崩了!"、"日志里全是异常但找不到原因"、"明明加了try-catch为什么还是有问题"...
如果你经常遇到这些情况,那么恭喜你,你已经踩进了C#异常处理的经典陷阱。作为一名有着10年开发经验的老程序员,我见过太多因为异常处理不当导致的线上故障。
今天这篇文章,我将用最直白的语言和最实用的代码,帮你彻底掌握C#异常处理的精髓,让你的代码从"脆弱易碎"变成"坚如磐石"。
💀 陷阱一:异常"黑洞" - 最危险的沉默杀手
问题分析
很多开发者为了"稳定",喜欢把所有异常都捕获然后什么都不做。这就像把烟雾报警器的电池拆掉一样危险!
C#// ❌ 死亡代码 - 异常黑洞
try
{
ProcessCriticalData();
}
catch
{
// 静默处理,什么都不做
}
✅ 正确解决方案
C#// ✅ 正确做法 - 记录日志并合理处理
try
{
ProcessCriticalData();
}
catch (SqlException ex)
{
_logger.LogError(ex, "数据库操作失败,订单ID: {OrderId}", orderId);
// 根据业务需求决定是否重新抛出
throw new BusinessException("订单处理失败,请联系客服", ex);
}
catch (Exception ex)
{
_logger.LogCritical(ex, "未知错误,需要紧急处理");
throw; // 重新抛出,让上层处理
}
在工业4.0时代,设备间的通信变得越来越重要。你是否也遇到过这样的痛点:需要与各种工业设备通信,但每个设备的协议都不一样?传统的COM、Modbus等协议配置复杂,维护困难?今天我们就用C#来打造一个现代化的OPC UA客户端,让设备通信变得简单优雅!
本文将带你从架构设计到界面实现,完整构建一个生产级的OPC UA Bridge应用。无论你是工业软件开发者,还是想了解现代C# WPF开发最佳实践的程序员,这篇文章都会让你收获满满。
🔍 问题分析:为什么选择OPC UA?
传统工业通信面临的三大痛点:
- 协议碎片化:不同厂商设备协议各异,集成困难
- 安全性不足:明文传输,易被攻击
- 可扩展性差:添加新设备需要重新开发
OPC UA作为新一代工业通信标准,完美解决了这些问题:
- 统一的通信协议和数据模型
- 内置安全机制
- 跨平台支持
🏗️ 架构设计:MVVM + 服务层的最佳实践
我们采用分层架构设计,确保代码的可维护性和可测试性:
Markdown📦 AppOPCUABridge ├── 📁 Models # 数据模型层 ├── 📁 Services # 业务服务层 ├── 📁 ViewModels # 视图模型层 ├── 📁 Views # 用户界面层 └── 📁 Converters # 数据转换器
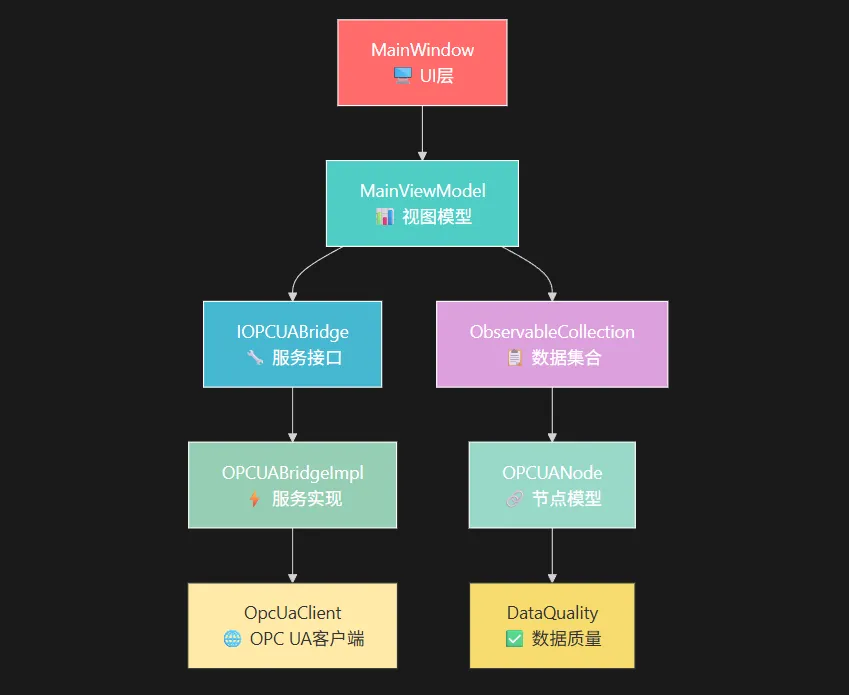
💎 核心模型设计
🎯 OPC UA节点模型
首先定义我们的核心数据模型,这是整个系统的基础:
C#public class OPCUANode : INotifyPropertyChanged
{
private string _nodeId;
private string _displayName;
private object _value;
private DataQuality _quality;
private DateTime _lastUpdate;
public string NodeId
{
get => _nodeId;
set
{
_nodeId = value;
OnPropertyChanged(nameof(NodeId));
}
}
public string DisplayName
{
get => _displayName;
set
{
_displayName = value;
OnPropertyChanged(nameof(DisplayName));
}
}
public object Value
{
get => _value;
set
{
_value = value;
LastUpdate = DateTime.Now;
OnPropertyChanged(nameof(Value));
}
}
public DataQuality Quality
{
get => _quality;
set
{
_quality = value;
OnPropertyChanged(nameof(Quality));
}
}
public DateTime LastUpdate
{
get => _lastUpdate;
set
{
_lastUpdate = value;
OnPropertyChanged(nameof(LastUpdate));
}
}
public ObservableCollection<OPCUANode> Children { get; set; }
= new ObservableCollection<OPCUANode>();
public event PropertyChangedEventHandler PropertyChanged;
protected virtual void OnPropertyChanged(string propertyName)
{
PropertyChanged?.Invoke(this, new PropertyChangedEventArgs(propertyName));
}
}