你是否在Python开发中遇到过这样的困扰：不同形状的数组无法直接进行运算？或者为了让两个数组能够相加，不得不写大量的循环代码？今天我们就来深入解析NumPy的数组广播机制，这个被誉为NumPy最强大特性之一的功能，将彻底改变你处理数值计算的方式。

广播机制不仅能让你告别繁琐的循环代码，更能让你的程序运行速度提升数倍。无论你是刚接触NumPy的新手，还是想要优化代码性能的资深开发者，掌握广播机制都将让你的Python开发技能更上一层楼。

🔍 问题分析：为什么需要数组广播？

传统方法的痛点

在没有广播机制之前，我们处理不同形状数组的运算时，往往需要手动扩展数组或使用循环：

Python
import numpy as np

# 传统方法：手动循环处理
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

scalar = 10

# 错误的做法：需要手动循环
result = np.zeros_like(matrix)
for i in range(matrix.shape[0]):
    for j in range(matrix.shape[1]):
        result[i, j] = matrix[i, j] + scalar

print("传统方法结果：")
print(result)

这种方法不仅代码冗长，执行效率也很低。在处理大型数据集时，性能问题会更加明显。

🎯 广播机制的核心价值

数组广播是NumPy提供的一种机制，它允许不同形状的数组在进行算术运算时，自动调整形状以匹配运算要求。这个过程是隐式的、高效的，无需手动干预。

💡 解决方案：深入理解广播规则

🔥 广播的三大黄金法则

NumPy的广播遵循以下规则，理解这些规则是掌握广播机制的关键：

法则1：维度对齐

从数组的最后一个维度开始比较
如果维度不匹配，在较小的数组前面补1

法则2：尺寸兼容

对应维度的大小要么相等
要么其中一个为1
要么其中一个不存在

法则3：结果形状

结果数组的形状是输入数组对应维度的最大值

让我们通过具体例子来理解：

Python
import numpy as np

# 示例1：标量与数组的广播
arr_2d = np.array([[1, 2, 3],
                   [4, 5, 6]])
scalar = 10

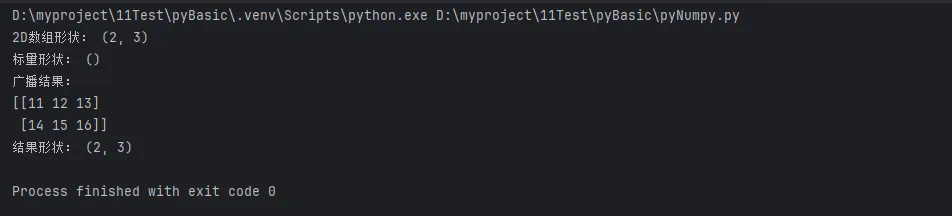
print("2D数组形状：", arr_2d.shape)  # (2, 3)
print("标量形状：", np.array(scalar).shape)  # ()

result = arr_2d + scalar
print("广播结果：")
print(result)
print("结果形状：", result.shape)  # (2, 3)

🎨 可视化广播过程

为了更好地理解广播机制，我们来看一个可视化的例子：

Python
import numpy as np

# 示例2：一维数组与二维数组的广播
arr_2d = np.array([[10, 20, 30],
                   [40, 50, 60]])

arr_1d = np.array([1, 2, 3])

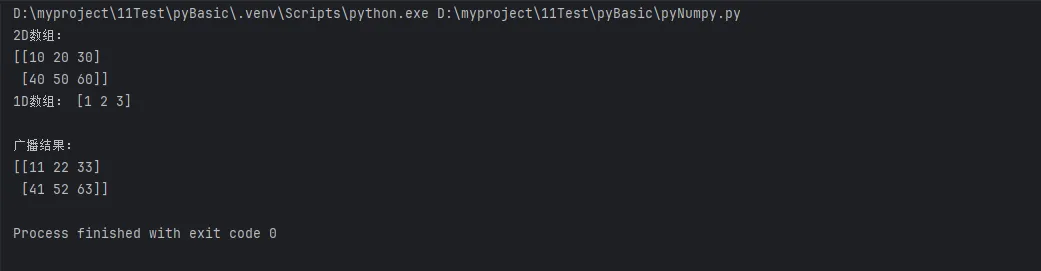
print("2D数组：")
print(arr_2d)
print("1D数组：", arr_1d)

# 广播过程分析：
# arr_2d: (2, 3)
# arr_1d: (3,) 

result = arr_2d + arr_1d
print("\n广播结果：")
print(result)

🛠️ 代码实战：广播机制的实际应用

🌟 实战案例1：数据标准化

在机器学习中，数据标准化是常见需求。广播机制让这个过程变得异常简单：

Python
import numpy as np

# 数据标准化实战
data = np.random.randn(1000, 5)  # 1000个样本，5个特征

# 计算每个特征的均值和标准差
mean = np.mean(data, axis=0)     # 形状：(5,)
std = np.std(data, axis=0)       # 形状：(5,)

print("原始数据形状：", data.shape)
print("均值形状：", mean.shape)
print("标准差形状：", std.shape)

# 利用广播进行标准化
normalized_data = (data - mean) / std

print("标准化后数据形状：", normalized_data.shape)
print("标准化后均值：", np.mean(normalized_data, axis=0))
print("标准化后标准差：", np.std(normalized_data, axis=0))

🚀 实战案例2：图像处理中的通道操作

在上位机开发中，图像处理是常见场景。广播机制在处理RGB图像时特别有用：

Python
import numpy as np

# 模拟RGB图像数据
image = np.random.randint(0, 256, (480, 640, 3), dtype=np.uint8)  # 高x宽x通道

# 定义每个通道的调整系数
channel_weights = np.array([0.8, 1.0, 1.2])  # R, G, B通道权重

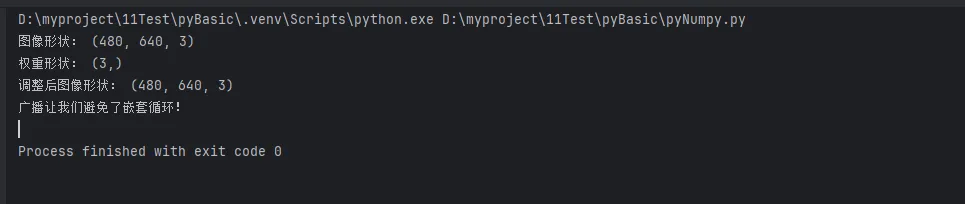
print("图像形状：", image.shape)   
print("权重形状：", channel_weights.shape)

# 利用广播调整各通道亮度
adjusted_image = image * channel_weights

print("调整后图像形状：", adjusted_image.shape)
print("广播让我们避免了嵌套循环！")

💰 实战案例3：金融数据分析

在量化交易或金融数据分析中，广播机制同样发挥重要作用：

Python
import numpy as np

# 模拟股票价格数据
# 10只股票，30天的价格数据
prices = np.random.uniform(10, 100, (30, 10))

# 计算基准日期的价格（第一天）
base_prices = prices[0, :]  # 形状：(10,)

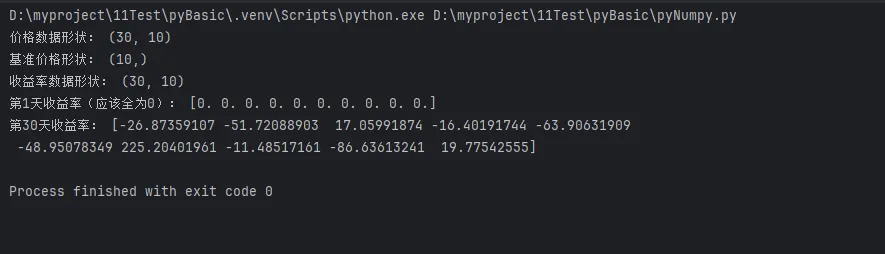
print("价格数据形状：", prices.shape)
print("基准价格形状：", base_prices.shape)

# 计算相对于基准日的涨跌幅
returns = (prices - base_prices) / base_prices * 100

print("收益率数据形状：", returns.shape)
print("第1天收益率（应该全为0）：", returns[0, :])
print("第30天收益率：", returns[-1, :])

⚡ 性能对比：广播 vs 循环

让我们来实际测试广播机制带来的性能提升：

Python
import numpy as np
import time

# 创建大型数组进行性能测试
large_array = np.random.randn(1000, 1000)
vector = np.random.randn(1000)

# 方法1：使用广播
start_time = time.time()
result_broadcast = large_array + vector
broadcast_time = time.time() - start_time

# 方法2：使用循环
start_time = time.time()
result_loop = np.zeros_like(large_array)
for i in range(large_array.shape[0]):
    result_loop[i, :] = large_array[i, :] + vector
loop_time = time.time() - start_time

print(f"广播方法耗时：{broadcast_time:.6f}秒")
print(f"循环方法耗时：{loop_time:.6f}秒")
print(f"性能提升：{loop_time/broadcast_time:.2f}倍")
print(f"结果一致性检查：{np.allclose(result_broadcast, result_loop)}")

🔧 高级技巧：自定义广播

有时我们需要更精确地控制广播行为：

Python
import numpy as np
import time

# 使用np.newaxis进行维度扩展
arr = np.array([1, 2, 3, 4])
print("原数组形状：", arr.shape)

# 转换为列向量
col_vector = arr[:, np.newaxis]
print("列向量形状：", col_vector.shape)

# 转换为行向量
row_vector = arr[np.newaxis, :]
print("行向量形状：", row_vector.shape)

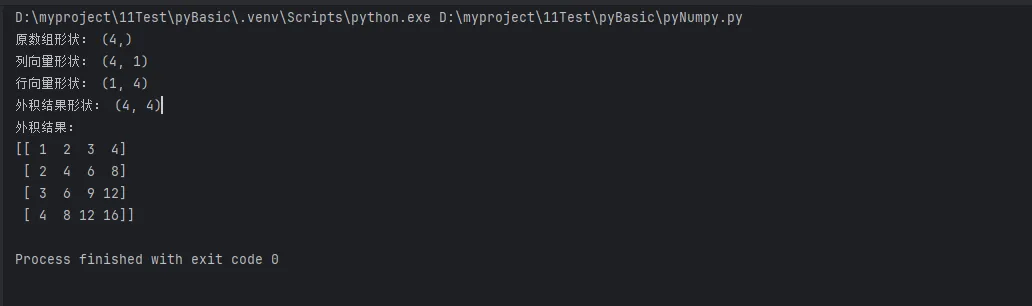
# 现在可以进行外积运算
outer_product = col_vector * row_vector
print("外积结果形状：", outer_product.shape)
print("外积结果：")
print(outer_product)

⚠️ 常见陷阱与最佳实践

🚨 广播失败的典型情况

Python
# 广播失败示例
try:
    arr1 = np.array([[1, 2, 3]])      # 形状：(1, 3)
    arr2 = np.array([[1], [2]])       # 形状：(2, 1)
    arr3 = np.array([1, 2])           # 形状：(2,)
    
    # 这个运算会失败
    result = arr1 + arr3
    print("运算成功")
except ValueError as e:
    print(f"广播失败：{e}")

# 正确的做法：
arr3_reshaped = arr3.reshape(1, 2)  # 重塑为 (1, 2)
# 或者使用 arr3[np.newaxis, :] 也可以

💡 性能优化建议

避免不必要的数组复制
预先规划数组形状
使用就地操作减少内存占用

Python
# 性能优化示例
large_matrix = np.random.randn(10000, 100)
adjustment = np.random.randn(100)

# 推荐：就地操作
large_matrix += adjustment  # 节省内存，提高性能

# 而不是：
# large_matrix = large_matrix + adjustment  # 会创建新数组

🎯 总结

通过本文的深入解析，我们掌握了NumPy数组广播机制的核心要点：

🔑 三个关键收获：

广播规则理解：掌握了维度对齐、尺寸兼容、结果形状的三大黄金法则，让你能够预测任何广播操作的结果
实战应用技巧：从数据标准化到图像处理，从金融分析到性能优化，广播机制在各种Python开发场景中都能显著提升代码效率
性能优势明显：相比传统循环方法，广播机制能带来数倍甚至数十倍的性能提升，特别适合处理大规模数据集

掌握广播机制不仅能让你的NumPy代码更加简洁优雅，更能在上位机开发、数据分析、机器学习等领域中发挥巨大作用。建议你在实际项目中多加练习，将这些技巧融入到日常的Python编程实践中。

延伸学习建议： 深入了解NumPy的向量化操作、内存布局优化，以及与Pandas、SciPy等科学计算库的协同使用，将进一步提升你的Python数值计算能力。

目录