技术老小子
🚀 Python NumPy线性代数运算：从入门到实战的完整指南
编辑
2025-11-26
Python
00

目录

🔍 问题分析：为什么选择NumPy进行线性代数运算？
💪 性能优势
🎯 内存效率
💡 解决方案：NumPy线性代数核心功能详解
🏗️ 基础矩阵操作
矩阵创建与初始化
矩阵基本运算
⚡ 高级线性代数运算
矩阵分解
特征值与特征向量
🔧 实战应用场景
线性方程组求解
最小二乘拟合
🛠️ 代码实战：完整项目示例
📊 图像处理中的线性变换
🎯 性能优化技巧
向量化操作优化
内存优化策略
🔥 高级应用与最佳实践
🚀 并行计算优化
🎯 总结

在Python开发中，特别是上位机开发和数据分析领域，线性代数运算是不可避免的核心技能。无论你是在处理传感器数据、图像处理，还是机器学习算法，NumPy的线性代数功能都能让你的代码更高效、更专业。

本文将从实战角度出发，详细解析Python NumPy中的线性代数运算，帮助你掌握从基础矩阵操作到高级数值计算的全套技能。我们不仅会讲解理论知识，更重要的是提供大量可直接应用于实际项目的编程技巧和最佳实践。

🔍 问题分析：为什么选择NumPy进行线性代数运算？

💪 性能优势

NumPy底层使用C语言实现，相比纯Python代码，运算速度提升10-100倍：

Python
import numpy as np
import time

# 纯Python矩阵乘法
def python_matrix_multiply(A, B):
    rows_A, cols_A = len(A), len(A[0])
    rows_B, cols_B = len(B), len(B[0])
    result = [[0 for _ in range(cols_B)] for _ in range(rows_A)]
    
    for i in range(rows_A):
        for j in range(cols_B):
            for k in range(cols_A):
                result[i][j] += A[i][k] * B[k][j]
    return result

# 测试数据
size = 500
A_py = [[1 for _ in range(size)] for _ in range(size)]
B_py = [[2 for _ in range(size)] for _ in range(size)]
A_np = np.ones((size, size))
B_np = np.ones((size, size)) * 2

# 性能对比
start = time.time()
result_py = python_matrix_multiply(A_py, B_py)
python_time = time.time() - start

start = time.time()
result_np = np.dot(A_np, B_np)
numpy_time = time.time() - start

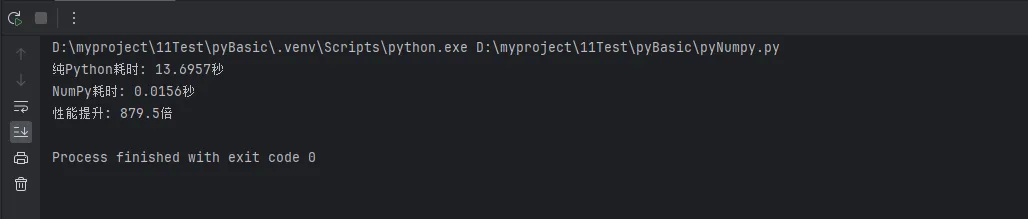
print(f"纯Python耗时: {python_time:.4f}秒")
print(f"NumPy耗时: {numpy_time:.4f}秒")
print(f"性能提升: {python_time/numpy_time:.1f}倍")

image.png

🎯 内存效率

NumPy数组在内存中连续存储，避免了Python列表的指针开销：

Python
import numpy as np
import time
import sys

# 内存使用对比
python_matrix = [[1.0 for _ in range(1000)] for _ in range(1000)]
numpy_matrix = np.ones((1000, 1000), dtype=np.float64)

python_size = sys.getsizeof(python_matrix) + sum(sys.getsizeof(row) for row in python_matrix)
numpy_size = numpy_matrix.nbytes

print(f"Python列表内存占用: {python_size/1024/1024:.2f}MB")
print(f"NumPy数组内存占用: {numpy_size/1024/1024:.2f}MB")
print(f"内存节省: {(python_size-numpy_size)/python_size*100:.1f}%")

image.png

💡 解决方案：NumPy线性代数核心功能详解

🏗️ 基础矩阵操作

矩阵创建与初始化

Python
import numpy as np

# 常用矩阵创建方法
zeros_matrix = np.zeros((3, 3))          # 零矩阵
ones_matrix = np.ones((3, 3))            # 全1矩阵
identity_matrix = np.eye(3)              # 单位矩阵
random_matrix = np.random.rand(3, 3)     # 随机矩阵
diagonal_matrix = np.diag([1, 2, 3])     # 对角矩阵

# 从列表创建
data = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix_from_list = np.array(data)

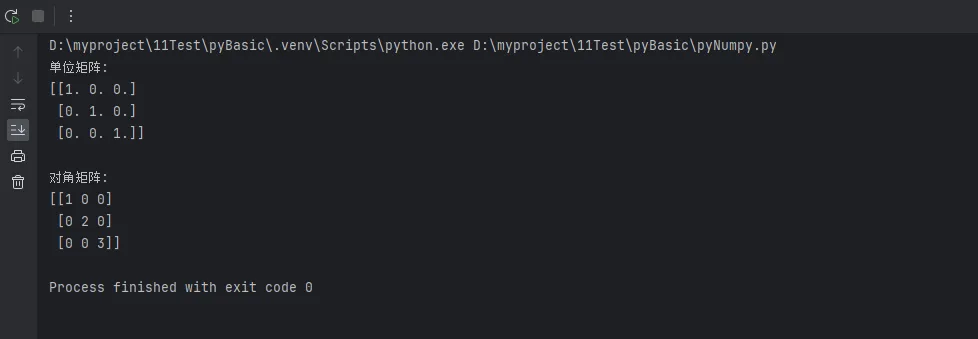
print("单位矩阵:")
print(identity_matrix)
print("\n对角矩阵:")
print(diagonal_matrix)

image.png

矩阵基本运算

Python
import numpy as np
import time
import sys

# 定义测试矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 基础运算
addition = A + B              # 矩阵加法
subtraction = A - B           # 矩阵减法
element_multiply = A * B      # 逐元素乘法
matrix_multiply = A @ B       # 矩阵乘法（推荐写法）
matrix_multiply2 = np.dot(A, B)  # 矩阵乘法（传统写法）

# 转置和共轭转置
transpose = A.T               # 转置
conjugate_transpose = A.conj().T  # 共轭转置

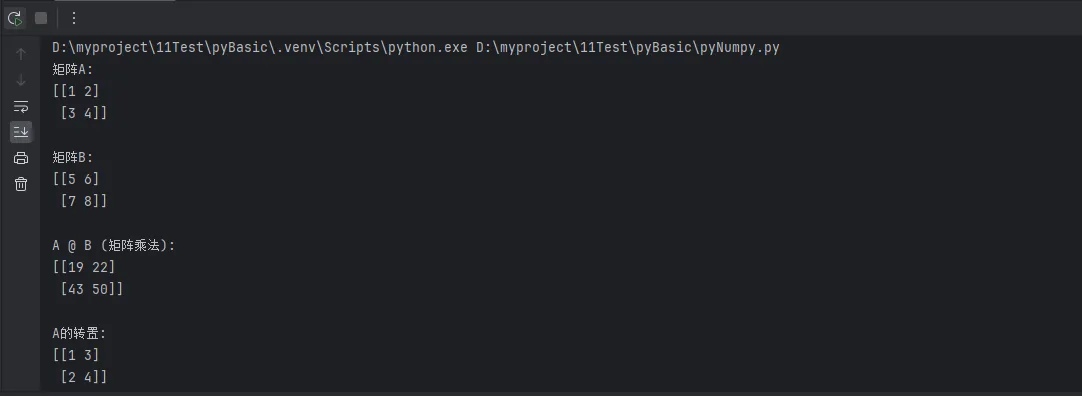
print("矩阵A:")
print(A)
print("\n矩阵B:")
print(B)
print("\nA @ B (矩阵乘法):")
print(matrix_multiply)
print("\nA的转置:")
print(transpose)

image.png

⚡ 高级线性代数运算

矩阵分解

Python
import numpy as np
import time
import sys

# LU分解示例
from scipy.linalg import lu

A = np.array([[2, 1, 1],
              [1, 3, 2],
              [1, 0, 0]], dtype=float)

P, L, U = lu(A)
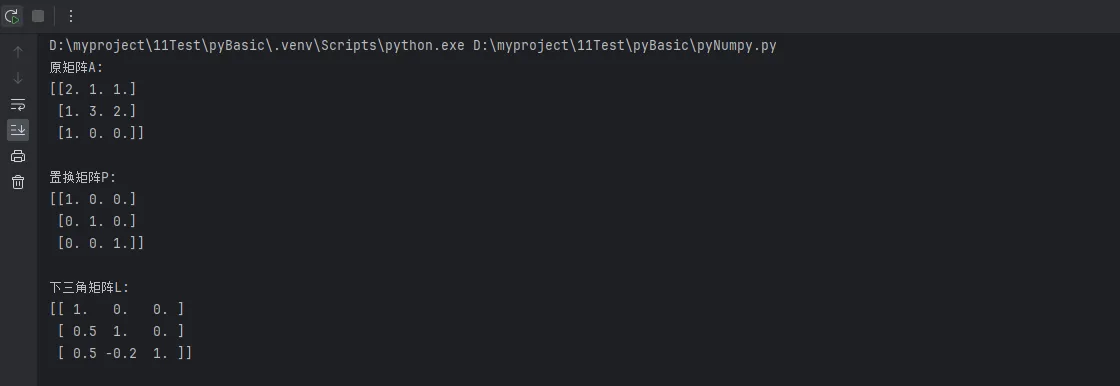
print("原矩阵A:")
print(A)
print("\n置换矩阵P:")
print(P)
print("\n下三角矩阵L:")
print(L)
print("\n上三角矩阵U:")
print(U)
print("\n验证P@L@U:")
print(P @ L @ U)

# QR分解
Q, R = np.linalg.qr(A)
print("\n正交矩阵Q:")
print(Q)
print("\n上三角矩阵R:")
print(R)
print("\n验证Q@R:")
print(Q @ R)

image.png

特征值与特征向量

Python
import numpy as np
import time
import sys

# 特征值分解
A = np.array([[4, 2],
              [1, 3]])

eigenvalues, eigenvectors = np.linalg.eig(A)

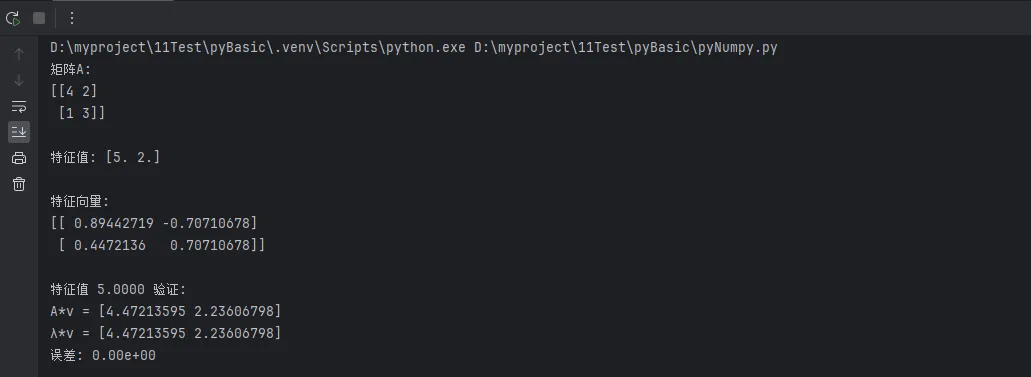
print("矩阵A:")
print(A)
print(f"\n特征值: {eigenvalues}")
print("\n特征向量:")
print(eigenvectors)

# 验证特征值特征向量关系
for i in range(len(eigenvalues)):
    lambda_i = eigenvalues[i]
    v_i = eigenvectors[:, i]

    # A * v = λ * v
    left_side = A @ v_i
    right_side = lambda_i * v_i

    print(f"\n特征值 {lambda_i:.4f} 验证:")
    print(f"A*v = {left_side}")
    print(f"λ*v = {right_side}")
    print(f"误差: {np.linalg.norm(left_side - right_side):.2e}")

image.png

🔧 实战应用场景

线性方程组求解

Python
# 实际工程问题：电路分析
# 假设有三个节点的电路，求各节点电压

# 系数矩阵（基于基尔霍夫定律）
A = np.array([[ 3, -1, -1],
              [-1,  4, -2],
              [-1, -2,  5]], dtype=float)

# 常数向量（电流源）
b = np.array([2, 1, 3], dtype=float)

# 求解方程组 A*x = b
voltages = np.linalg.solve(A, b)

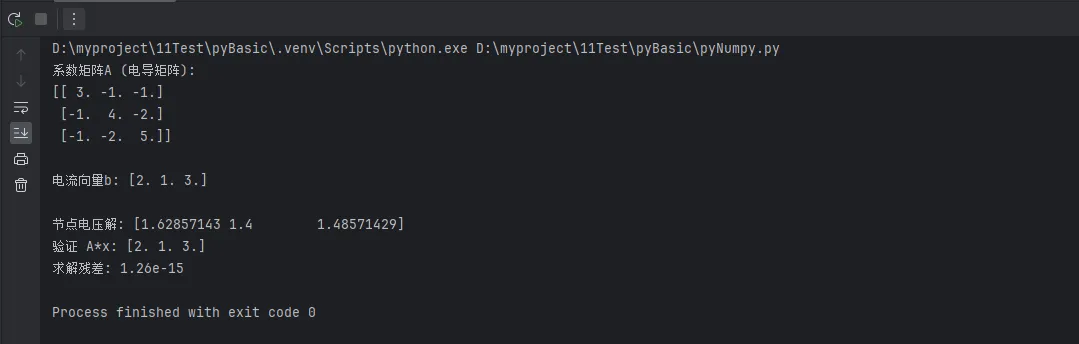
print("系数矩阵A (电导矩阵):")
print(A)
print(f"\n电流向量b: {b}")
print(f"\n节点电压解: {voltages}")
print(f"验证 A*x: {A @ voltages}")

# 检查解的准确性
residual = np.linalg.norm(A @ voltages - b)
print(f"求解残差: {residual:.2e}")

image.png

最小二乘拟合

Python
import numpy as np
import time
import sys

# 数据拟合问题：传感器数据线性化
np.random.seed(42)

# 模拟传感器数据（带噪声）
x_data = np.linspace(0, 10, 50)
true_slope, true_intercept = 2.5, 1.2
noise = np.random.normal(0, 0.5, len(x_data))
y_data = true_slope * x_data + true_intercept + noise

# 构造设计矩阵
X = np.column_stack([x_data, np.ones(len(x_data))])  # [x, 1] for ax+b
y = y_data

# 最小二乘解：(X^T * X)^(-1) * X^T * y
coefficients = np.linalg.lstsq(X, y, rcond=None)[0]
fitted_slope, fitted_intercept = coefficients

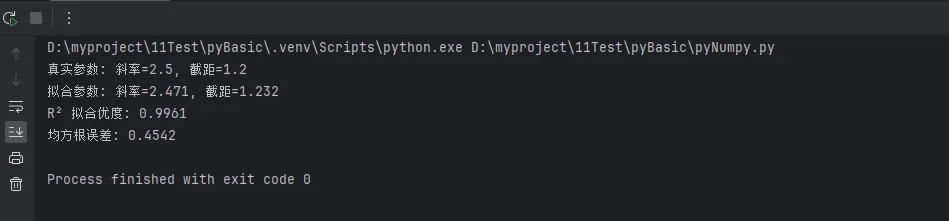
print(f"真实参数: 斜率={true_slope}, 截距={true_intercept}")
print(f"拟合参数: 斜率={fitted_slope:.3f}, 截距={fitted_intercept:.3f}")

# 计算拟合优度
y_pred = X @ coefficients
r_squared = 1 - np.sum((y - y_pred)**2) / np.sum((y - np.mean(y))**2)
print(f"R² 拟合优度: {r_squared:.4f}")

# 残差分析
residuals = y - y_pred
rms_error = np.sqrt(np.mean(residuals**2))
print(f"均方根误差: {rms_error:.4f}")

image.png

🛠️ 代码实战：完整项目示例

📊 图像处理中的线性变换

Python
import matplotlib.pyplot as plt

# 模拟图像变换项目
def create_test_image():
    """创建测试图像"""
    x = np.linspace(-2, 2, 100)
    y = np.linspace(-2, 2, 100)
    X, Y = np.meshgrid(x, y)
    
    # 创建简单的几何图形
    image = (X**2 + Y**2 < 1).astype(float)  # 圆形
    return image, X, Y

def apply_linear_transformation(points, transform_matrix):
    """应用线性变换"""
    # points shape: (2, N) for 2D points
    # transform_matrix shape: (2, 2)
    return transform_matrix @ points

# 创建测试图像
image, X, Y = create_test_image()

# 定义变换矩阵
rotation_angle = np.pi / 4  # 45度旋转
rotation_matrix = np.array([[np.cos(rotation_angle), -np.sin(rotation_angle)],
                           [np.sin(rotation_angle),  np.cos(rotation_angle)]])

scaling_matrix = np.array([[1.5, 0],    # x方向放大1.5倍
                          [0, 0.8]])     # y方向缩小到0.8倍

shear_matrix = np.array([[1, 0.3],       # x方向剪切
                        [0, 1]])

# 组合变换：先缩放，再旋转，最后剪切
combined_transform = shear_matrix @ rotation_matrix @ scaling_matrix

print("旋转矩阵 (45度):")
print(rotation_matrix)
print("\n缩放矩阵:")
print(scaling_matrix)
print("\n剪切矩阵:")
print(shear_matrix)
print("\n组合变换矩阵:")
print(combined_transform)

# 计算变换的行列式（面积变化因子）
det = np.linalg.det(combined_transform)
print(f"\n变换行列式: {det:.3f}")
print(f"面积变化: {abs(det):.1f}倍")

image.png

🎯 性能优化技巧

向量化操作优化

Python
def performance_comparison():
    """性能优化对比"""
    size = 10000
    
    # 创建大型矩阵
    A = np.random.rand(size, size)
    B = np.random.rand(size, size)
    
    # 方法1：循环计算（慢）
    def slow_matrix_operation():
        result = np.zeros_like(A)
        for i in range(size):
            for j in range(size):
                result[i, j] = A[i, j] * B[i, j] + np.sin(A[i, j])
        return result
    
    # 方法2：向量化操作（快）
    def fast_matrix_operation():
        return A * B + np.sin(A)
    
    # 只在小规模上测试循环版本
    small_size = 100
    A_small = A[:small_size, :small_size]
    B_small = B[:small_size, :small_size]
    
    # 测试向量化版本
    start = time.time()
    result_fast = fast_matrix_operation()
    fast_time = time.time() - start
    
    print(f"向量化操作耗时: {fast_time:.4f}秒")
    print("向量化操作是NumPy的核心优势！")

performance_comparison()

image.png

内存优化策略

Python
import numpy as np
import time
import sys


def memory_optimization_demo():
    """内存优化演示"""

    # 原地操作 vs 创建新数组
    large_array = np.random.rand(5000, 5000)

    # 方法1：创建新数组（占用更多内存）
    def memory_intensive():
        result = large_array * 2
        result = result + 1
        result = np.sin(result)
        return result

    # 方法2：原地操作（节省内存）
    def memory_efficient():
        np.multiply(large_array, 2, out=large_array)  # 原地乘法
        np.add(large_array, 1, out=large_array)  # 原地加法
        np.sin(large_array, out=large_array)  # 原地sin
        return large_array

    # 使用适当的数据类型
    # float64 vs float32
    arr_64 = np.random.rand(1000000).astype(np.float64)
    arr_32 = np.random.rand(1000000).astype(np.float32)

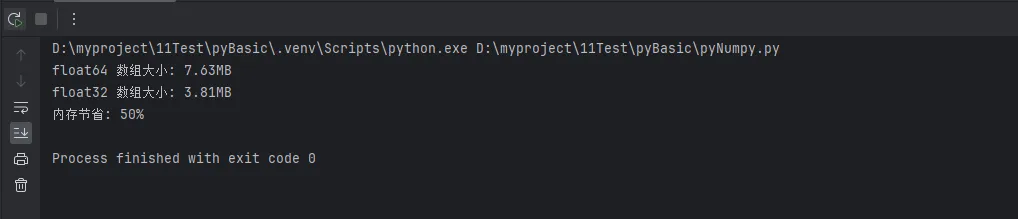
    print(f"float64 数组大小: {arr_64.nbytes / 1024 / 1024:.2f}MB")
    print(f"float32 数组大小: {arr_32.nbytes / 1024 / 1024:.2f}MB")
    print(f"内存节省: {50:.0f}%")


memory_optimization_demo()

image.png

🔥 高级应用与最佳实践

🚀 并行计算优化

Python
import numpy as np
import time
import sys

# 利用NumPy的多线程能力
import os

os.environ['OMP_NUM_THREADS'] = '4'  # 设置OpenMP线程数


def parallel_computation_demo():
    """并行计算演示"""

    # 大规模矩阵运算
    n = 2000
    A = np.random.rand(n, n)
    B = np.random.rand(n, n)
    C = np.random.rand(n, n)

    # 复杂的矩阵运算链
    start = time.time()
    result = (A @ B @ C + A.T @ B) @ np.linalg.inv(A + np.eye(n) * 0.1)
    parallel_time = time.time() - start

    print(f"并行矩阵运算耗时: {parallel_time:.4f}秒")
    print(f"结果矩阵形状: {result.shape}")

    # 检查数值稳定性
    condition_number = np.linalg.cond(A)
    print(f"矩阵条件数: {condition_number:.2e}")

    if condition_number > 1e12:
        print("⚠️  警告：矩阵接近奇异，结果可能不稳定")
    else:
        print("✅ 矩阵条件良好，结果可信")


parallel_computation_demo()

image.png

🎯 总结

通过本文的深入学习，我们掌握了Python NumPy线性代数运算的三个核心要点：

  1. 性能优化：利用NumPy的向量化操作和并行计算能力，实现10-100倍的性能提升，这对上位机开发和实时数据处理至关重要。
  2. 实战应用：从电路分析到图像变换，从数据拟合到特征提取，线性代数为各种Python开发场景提供了强大的数学工具支持。
  3. 工程实践：通过健壮的错误处理、内存优化和性能监控，确保代码在生产环境中的稳定性和可靠性。

掌握这些编程技巧不仅能让你的代码更加专业和高效，更能为你在数据科学、机器学习、科学计算等领域的发展奠定坚实基础。NumPy的线性代数功能是现代Python技术栈中不可或缺的核心组件，值得每一位Python开发者深入掌握。

继续实践和探索，你将发现NumPy在解决复杂技术问题时的无限可能！

💡 想了解更多Python高级技巧？关注我们，获取最新的Python开发**实战教程和编程技巧**分享！

本文作者:技术老小子

本文链接:

版权声明:本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！